Cho tam giác ABC vuông tại A (AB < AC). Vẽ tia phân giác Ax. Vẽ BD vuông góc với Ax tại D và CE vuông góc với Ax tại E. Gọi M là trung điểm của BC. Tính các góc của tam giác DME.

Trả lời

Lời giải

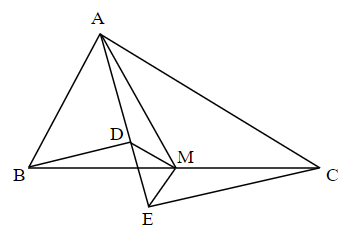
Xét ΔABC có: $\widehat A = 90^\circ$; M là trung điểm BC.

Suy ra AM = BM = CM.

Vì Ax là tia phân giác $\widehat {BAC}$ nên $\widehat {BAD} = \widehat {CAE} = 45^\circ$.

Mà BD ⊥ Ax, CE ⊥ Ax nên ∆BAD và ∆CAE lần lượt vuông cân tại D và E.

Do đó DA = DB và EA = EC.

Ta có ΔAEM = ΔCEM (c.c.c)

Suy ra $\widehat {AEM} = \widehat {CEM}$ (hai góc tương ứng)

⇒ EM là phân giác $\widehat {AEC}$ ⇒ $\widehat {AEM} = \widehat {CEM} = \frac{{90^\circ }}{2} = 45^\circ$ hay $\widehat {DEM} = 45^\circ$.

Ta có: $\widehat {BDM} = \widehat {BDE} + \widehat {EDM} = 90^\circ + \widehat {EDM} \Rightarrow \widehat {ADM} = 90^\circ + \widehat {EDM}$.

Lại có: $\widehat {ADM} + \widehat {EDM} = 180^\circ$ (hai góc kề bù).

Thay$\widehat {ADM} = 90^\circ + \widehat {EDM}$, ta được:

$90^\circ + \widehat {EDM} + \widehat {EDM} = 180^\circ$

$2\,\widehat {EDM} = 90^\circ \Rightarrow \widehat {EDM} = 45^\circ$.

Vậy ∆DME có $\widehat {DEM} = 45^\circ$; $\widehat {EDM}$ ⇒ $\widehat {DME} = 90^\circ$.