Cho tam giác ABC vuông tại A (AB < AC) đường cao AH. Trên tia HC lấy điểm D
Cho tam giác ABC vuông tại A (AB < AC) đường cao AH. Trên tia HC lấy điểm D sao cho HD = HA. Từ điểm D, vẽ đường thẳng vuông góc với BC cắt AC ở E. Chứng minh rằng AE = AB.
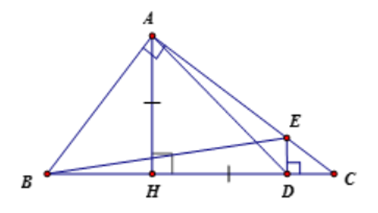
Tam giác AHD có:
HA = HD; \(\widehat {AHD} = 90^\circ \)
Do đó, tam giác AHD vuông cân
Do đó, \(\widehat {HDA} = 45^\circ \)
Tam giác CED và tam giác CBA có:
Góc \(\widehat C\) chung
\(\widehat D = \widehat A = 90^\circ \)
Do đó, tam giác CED đồng dạng với tam giác CBA (g.g)
\( \Rightarrow \frac{{CD}}{{CA}} = \frac{{CE}}{{CB}} \Rightarrow \frac{{CD}}{{CE}} = \frac{{CA}}{{CB}}\)
Xét tam giác CAD và tam giác CBE có:
\(\widehat C\) chung
\(\frac{{CD}}{{CE}} = \frac{{CA}}{{CB}}\)
Do đó, tam giác CAD đồng dạng với tam giác CBE (c.g.c)
Do đó, \(\widehat {BEC} = \widehat {ADC}\)
Ta có: \(\widehat {ADC} + \widehat {HDA} = 180^\circ \); \(\widehat {BEC} + \widehat {BEA} = 180^\circ \Rightarrow \widehat {BEC} = \widehat {ADC}\)
\( \Rightarrow \widehat {HDA} = \widehat {BEA}\) mà \(\widehat {HDA} = 45^\circ \)
\( \Rightarrow \widehat {BEA} = 45^\circ \)
Tam giác ABE có: \(\widehat A = 90^\circ ;\,\,\widehat {BEA} = 45^\circ \)
Do đó, tam giác ABE vuông cân
Do đó, AB = AE.