Lời giải
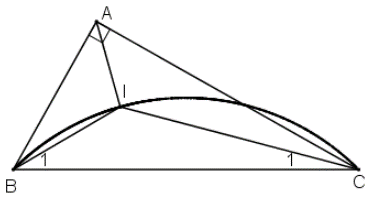
Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc 135º dựng trên đoạn BC.
⇒ I thuộc cung chứa góc 135º dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC.
+ Kẻ tia Bx sao cho BI là phân giác của \(\widehat {ABC}\).
+ Kẻ tia Cy sao cho CI là phân giác của \[\widehat {ACB}\].
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC.
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận: Quỹ tích điểm I là toàn bộ cung chứa góc 135º dựng trên đoạn BC (khác B và C).