Cho tam giác ABC, với M, N, P lần lượt là trung điểm BC, CA, AB. Khẳng định nào sau đây sai? A. vecto AB + vecto BC + vecto CA = vec 0; B. vecto AP + vecto BM + vecto CN = vec 0;
33
15/05/2024
Cho tam giác ABC, với M, N, P lần lượt là trung điểm BC, CA, AB. Khẳng định nào sau đây sai?
A. →AB+→BC+→CA=→0;
B. →AP+→BM+→CN=→0;
C. →MN+→NP+→PM=→0;
D. →PB+→MC=→MP.
Trả lời
Lời giải
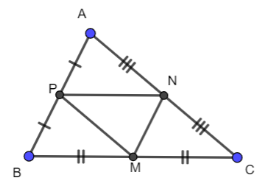
⦁ Ta có →AB+→BC+→CA=→AC+→CA=→AA=→0.
Do đó phương án A đúng.
⦁ Ta có →AP+→BM+→CN=→PB+→BM+→CN=→PM+→CN=→0 (vì PM là đường trung bình của tam giác ABC nên →PM=−→CN).
Do đó phương án B đúng.
⦁ Ta có →MN+→NP+→PM=→MP+→PM=→MM=→0.
Do đó phương án C đúng.
⦁ Ta có →PB+→MC=→PB+→BM=→PM≠→MP.
Do đó phương án D sai.
Vậy ta chọn phương án D.

