Cho tam giác ABC với AB = AC. Lấy I là trung điểm BC. Trên tia BC lấy điểm N, trên tia CB lấy điểm M sao cho CN = BM. Chứng minh:
a) ^ABI=^ACIvà AI là tia phân giác của góc BAC.
b) AM = AN.
c) AI vuông góc với BC.
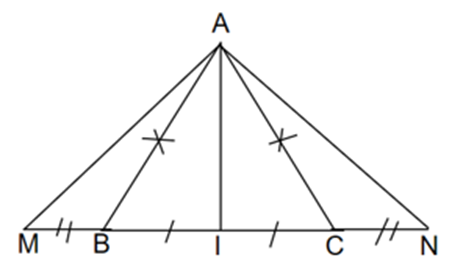
a) Xét △ABI và △ACI có
AI là cạnh chung
AB = AC (giả thiết)
BI = CI (giả thiết)
Suy ra △ABI = △ACI (c.c.c)
Do đó ^ABI=^ACI, ^BAI=^CAI (các góc tương ứng)
Suy ra AI là tia phân giác của góc BAC
b) Ta có ^ABI+^ABM=180∘ (hai góc kề bù)
^ACI+^ACN=180∘ (hai góc kề bù)
Mà ^ABI=^ACI(chứng minh câu a)
Suy ra ^ABM=^ACN
Xét △ABM và △ACN có
AB = AC (giả thiết)
^ABM=^ACN (chứng minh trên)
BM = CN (giả thiết)
Suy ra △ABM = △ACN (c.g.c)
Do đó AM = AN (hai cạnh tương ứng)
c) Vì △ABI = △ACI (chứng minh câu a)
Nên ^AIB=^AIC(hai góc tương ứng)
Mà ^AIB+^AIC=180∘(hai góc kề bù)
Suy ra ^AIB=^AIC=90∘
Hay AI ⊥ BC
Vậy AI ⊥ BC.