Cho tam giác ABC, vẽ AH vuông góc vs BC (H thuộc BC), trên tia AH lấy D sao cho
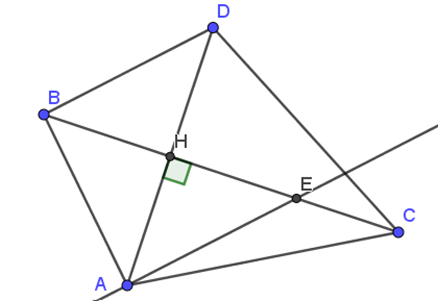
Cho tam giác ABC, vẽ AH vuông góc vs BC (H thuộc BC), trên tia AH lấy D sao cho AH = HD. Chứng minh:
a) Tam giác ABH bằng tam giác DBH.
b) AC = CD.
c) Qua A kẻ đg thẳng song song vs BD cắt BC tại E. Chứng minh H là trung điểm của BE.