Cho tam giác ABC và tam giác A’B’C’ có trọng tâm lần lượt là G và G’. Chứng minh rằng \[\overrightarrow {{\rm{AA'}}} + \overrightarrow {BB'} + \overrightarrow {CC'} = 3\overrightarrow {GG'} \]. Từ đó suy ra điều kiện cần và đủ để hai tam giác có cùng trọng tâm.

Vì G là trọng tâm của ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = 0\)

Vì G’ là trọng tâm của A’B’C’ nên \(\overrightarrow {G'A'} + \overrightarrow {G'B} ' + \overrightarrow {G'C} ' = 0\)

Ta có:

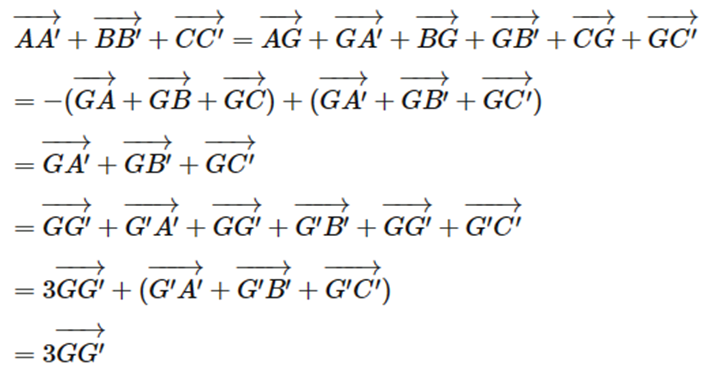
Suy ra điều kiện cần và đủ để hai tam giác có cùng trọng tâm (G trùng G’) là

\[\overrightarrow {{\rm{AA'}}} + \overrightarrow {BB'} + \overrightarrow {CC'} = \overrightarrow 0 \].