Cho tam giác ABC, trực tâm H, M là trung điểm BC. Chứng minh vecto MH. vecto MA
Cho tam giác ABC, trực tâm H, M là trung điểm BC. Chứng minh →MH.→MA=14BC2.
Cho tam giác ABC, trực tâm H, M là trung điểm BC. Chứng minh →MH.→MA=14BC2.
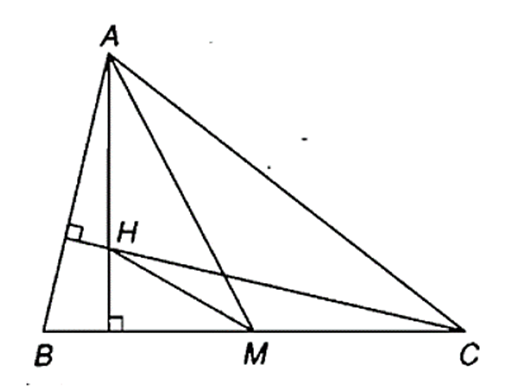
Vì M là trung điểm BC nên: {→AM=12(→AB+→AC)→HM=12(→HB+→HC)
Có: →MH.→MA=→AM.→HM
=14(→AB+→AC)(→HB+→HC)
=14(→AB.→HB+→AC.→HB+→AB.→HC+→AC.→HC)(do AC vuông góc HB nên →AC.→HB=→AB.→HC=→0)
=14(→AB.→HB+→AC.→HC)
=14(→HB(→AC−→BC)+→HC(→AB+→BC))
=14(→HB.→AC−→HB.→BC+→HC.→AB+→HC.→BC)
=14(−→HB.→BC+→HC.→BC)
=14→BC(−→HB+→HC)
=14→BC.→BC=14BC2.