Cho tam giác ABC, trọng tâm G.

a) Vẽ đường thẳng d qua G, cắt các đoạn thẳng AB, AC. Gọi A', B', C' là hình chiếu của A, B, C trên d. Tìm liên hệ giữa các độ dài AA', BB', CC'

b) Nếu đường thẳng d nằm ngoài tam giác ABC và G' là hình chiếu của G trên d thì các độ dài AA', BB', CC', GG' có liên hệ gì?

Lời giải

a)

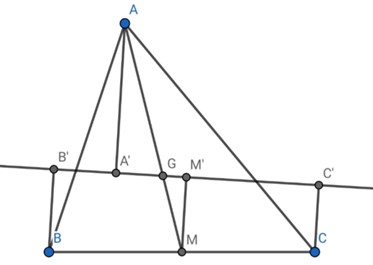
Gọi M là trung điểm của BC

M' là hình chiếu của M lên d

Þ MM' // BB' // CC'

Þ MM' là đường trung bình của hình thang vuông BB'C'C

$\Rightarrow MM' = \frac{1}{2}\left( {BB' + CC'} \right)$

Xét ∆AA'G và ∆MM'G có:

$\widehat {A'} = \widehat {M'} = 90^\circ$

$\widehat {A'AG} = \widehat {MM'G}$ (so le trong)

Do đó ∆AA'G ᔕ ∆MM'G (g.g)

$\Rightarrow \frac{{AA'}}{{MM'}} = \frac{{AG}}{{GM}}$

Áp dụng tính chất của trọng tâm, ta có:

$\frac{{AG}}{{AM}} = \frac{2}{3} \Rightarrow \frac{{AG}}{{GM}} = 2$

Do đó: $\frac{{AA'}}{{MM'}} = 2$

$\Rightarrow AA' = 2MM' = 2 \cdot \frac{1}{2}\left( {BB' + CC'} \right) = BB' + CC'$

Vậy AA' = BB' + CC'.

b)

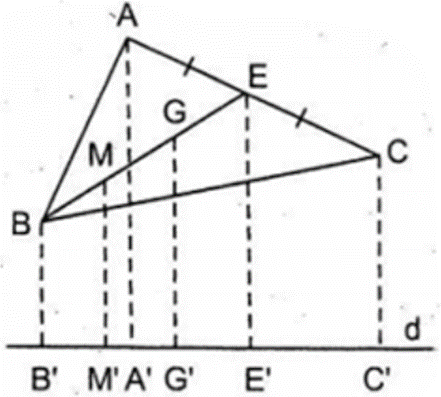
Gọi BE là đường trung tuyến của của AC, M là trung điểm của BG.

Vẽ AA', BB', CC', II', MM' vuông góc với d.

Ta có: G là trọng tâm của tam giác ABC nên suy ra

$\frac{{BG}}{{BE}} = \frac{2}{3} \Rightarrow \frac{{BG}}{{GE}} = 2 \Rightarrow \frac{{2.MG}}{{GE}} = 2$

$\Leftrightarrow \frac{{MG}}{{GE}} = 1 \Rightarrow \frac{{MG}}{{ME}} = \frac{1}{2}$

Suy ra G là trung điểm của ME

M', G', E' là hình chiếu của M, G, E lên d

Þ MM' // GG' // EE'

Þ GG' là đường trung bình của hình thang vuông MM'E'E

Chứng minh tương tự ta có MM' là đường trung bình của hình thang vuông BB'G'G.

Và EE' là đường trung bình của hình thang vuông AA'C'C.

Khi đó ta có:

MM' + EE' = 2GG'

Þ 2MM' + 2EE' = 4GG'

Þ BB' + GG' + AA' + CC' = 4GG'

Þ AA' + BB' + CC' = 3GG'