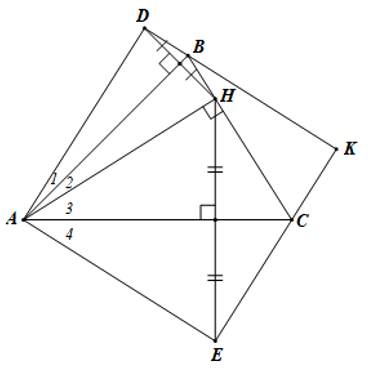
Cho tam giác ABC nhọn có góc $\widehat{A}=45°$ , đường cao AH. Điểm D đối xứng với H qua AB. Điểm E đối xứng với H qua AC. Điểm K là giao điểm của DB và EC. 

a) ADKE là hình gì ?

a)

Ta có H và D đối xứng nhau qua AB nên AD = AH; BH = BD và AB là tia phân giác của $\widehat{DAH}$

Suy ra $\widehat{A_1}=\widehat{A_2}=\frac{1}{2}\widehat{DAH}$

Ta có H  và E đối xứng nhau qua AC nên AH = AE; CH = CE và AC là tia phân giác của $\widehat{E\text{AH}}$

Suy ra $\widehat{A_3}=\widehat{A_4}=\frac{1}{2}\widehat{EAH}$

Vì AD = AH, AH = AE nên AD = AE

Ta có $\widehat{DAE}=\widehat{DAH}+\widehat{HA\text{E}}=2\widehat{A_2}+2\widehat{A_3}=2\left(\widehat{A_2}+\widehat{A_3}\right)=2.45°=90°$

Xét ΔADB và ΔAHB có 

AD = AH (chứng minh trên);

DB = HB (chứng minh trên);

AB chung

Do đó ΔADB = ΔAHB (c.c.c)

Suy ra  $\widehat{A\text{D}B}=\widehat{AHB}$(hai góc tương ứng)

Mà $\widehat{AHB}=90°$  nên $\widehat{A\text{D}B}=90°$

Tương tự ta cũng có $\widehat{AEC}=90°$

Xét tứ giác ADKE có  $\widehat{A\text{D}B}=\widehat{DA\text{E}}=\widehat{A\text{E}C}=90°$

Do đó ADKE là hình chữ nhật

Mà AD = AE (chứng minh trên)

Suy ra ADKE là hình vuông.