Cho tam giác ABC nhọn, BD vuông góc với AC, D thuộc AC, CE vuông góc
Cho tam giác ABC nhọn, BD vuông góc với AC, D thuộc AC, CE vuông góc với AB, E thuộc AB, BD cắt CE tại I. Chứng minh góc BIC bù góc A.
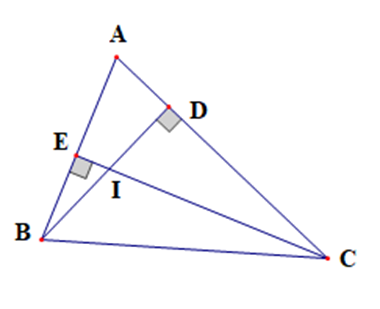
Vì tam giác BEC vuông tại E nên \(\widehat {EBC} + \widehat {ECB} = 90^\circ \) (trong tam giác vuông tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {ICB} = 90^\circ - \widehat {EBC}\)
Vì tam giác BCD vuông tại D nên \(\widehat {DBC} + \widehat {DCB} = 90^\circ \) (trong tam giác vuông tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {IBC} = 90^\circ - \widehat {DCB}\)
Xét tam giác BIC có
\(\widehat {BIC} + \widehat {ICB} + \widehat {IBC} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {BIC} + 90^\circ - \widehat {EBC} + 90^\circ - \widehat {DCB} = 180^\circ \)
Hay \(\widehat {BIC} = \widehat {EBC} + \widehat {DCB}\)
Mà \(\widehat {BAC} + \widehat {EBC} + \widehat {DCB} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {BIC} = 180^\circ - \widehat {CAB}\)
Vậy góc BIC bù góc A.