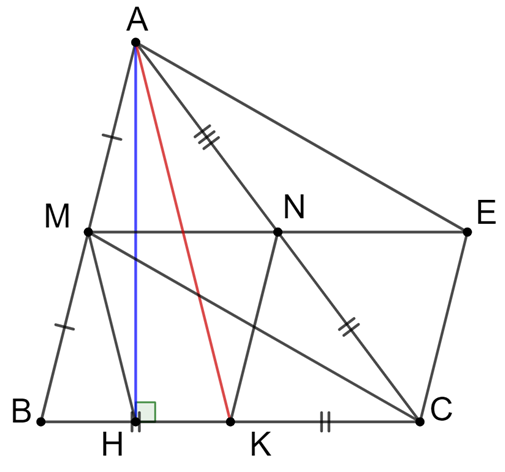
Cho tam giác ABC nhọn (AB < AC). Gọi M, N, K lần lượt là trung điểm của AB, AC, BC. Đường cao AH
a) Chứng minh tứ giác MNKH là hình thang cân
b) Gọi E là điểm đối xứng của M qua N. Tứ giác AMCE là hình gì?
c) Tam giác ABC cần có thêm điều kiện gì thì tứ giác AECM là hình chữ nhật?
a) Xét ΔABC có:
M là trung điểm AB
N là trung điểm AC
Þ MN là đường trung bình của tam giác ABC
Þ MN // BC và \(MN = \frac{{BC}}{2}\)
Xét ΔAHC có HN là trung tuyến
Þ \(HN = AN = NC = \frac{{AC}}{2}\)
Xét ΔABC có:
M là trung điểm AB
K là trung điểm BC
Þ MK là đường trung bình
Þ MK // AC và \(MK = \frac{{AC}}{2}\)
Þ MK = NH
Xét tứ giác MNKH có:
MN // HK
MK = NH
Suy ra MNKH là hình thang cân
b) E là điểm đối xứng của M qua N Þ MN = NE
Tứ giác AMCE có hai đường chéo AC và ME cắt nhau tại N.
Mà AN = NC (N là trung điểm của AC)
Và MN = NE (cmt)
Vậy AMCE là hình bình hành
c) Để hình bình hành AMCE là hình chữ nhật thì \(\widehat {AMC} = 90^\circ \)
Hay \(CM \bot AB\)
Mà CM là đường trung tuyến của tam giác ABC nên tam giác CAB cân tại C.