Cho tam giác ABC nhọn (AB < AC). Đường tròn tâm O, đường kính BC lần lượt cắt AB
53
05/05/2024
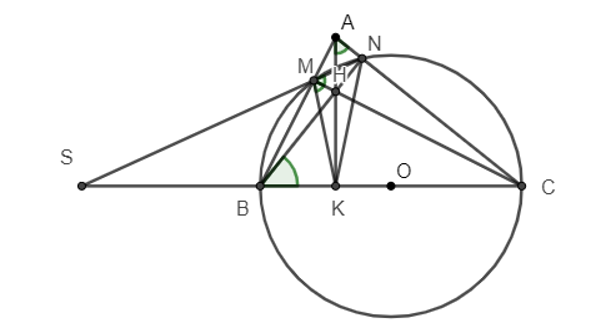
Cho tam giác ABC nhọn (AB < AC). Đường tròn tâm O, đường kính BC lần lượt cắt AB, AC tại M và N; BN và CM giao nhau tại H, AH cắt BC tại K.
a) Chứng minh: .
b) Chứng minh: AM.AB = AN.AC
c) Chứng minh: MH là phân giác góc NMK.
d) MN và BC cắt nhau tại S. Chứng minh: SB.SC = SK. SO
Trả lời
a) Ta có: BC là đường kính của (O) suy ra , .
Mà suy ra H là trực tâm tam giác
(đpcm)
b) Ta có:
(đpcm)
c) Ta có:
.
Suy ra ta có những tứ giác sau là những tứ giác nội tiếp:
AMHN, MHKB, ANKB.
Suy ra MH là phân giác góc NMK.
d) Ta có:
Suy ra
(g.g)
(1)
Theo câu c)
Suy ra MNOK nội tiếp.
(g.g)
(2)
Từ (1) và (2) suy ra:
SB.SC= SK.SO