Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB và O là 1 điểm tùy ý.
a) Chứng minh rằng: \(\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \overrightarrow 0 \).
b) Chứng minh rằng: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \).
a) Xét tam giác ABC có M là trung điểm của BC, P là trung điểm của AB
Suy ra MP là đường trung bình
Do đó MP // AC, \(MP = \frac{1}{2}AC\)
Mà N là trung điểm của AC nên \(NC = \frac{1}{2}AC\)
Suy ra \(\overrightarrow {PM} = \overrightarrow {NC} \)
Ta có: \(\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} \)
= \(\overrightarrow 0 \)
Vậy \(\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \overrightarrow 0 \)
b) Ta có:
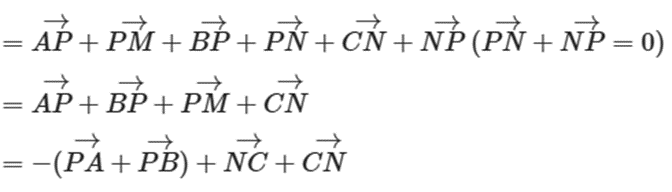
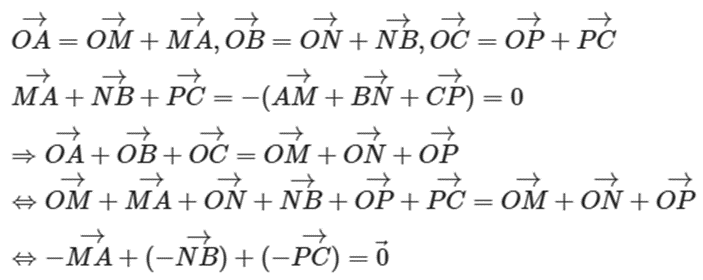
⇔ \(\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \overrightarrow 0 \) (đã chứng minh câu a)
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \).