Cho tam giác ABC, đường cao AH.

Biết \(AB = 4\;cm,\;AC = 4\sqrt 2 \;cm,\;BC = 4\sqrt 3 \;cm.\) Chứng minh tam giác ABC vuông. Tính độ dài các đoạn thẳng AH, HB.

Lời giải

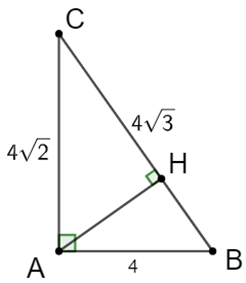
Theo hệ thức lượng trong tam giác ABC vuông tại A có AH là đường cao nên ta có:

• AH.BC = AB.AC

Suy ra \(AH = \frac{{AB\,.\,AC}}{{BC}} = \frac{{4\,\,.\,\,4\sqrt 2 }}{{4\sqrt 3 }} = \frac{{4\sqrt 6 }}{3}\;\,(cm)\).

• AB² = HB.BC

Suy ra \(HB = \frac{{A{B^2}}}{{BC}} = \frac{{{4^2}}}{{4\sqrt 3 }} = \frac{{4\sqrt 3 }}{3}\;\,(cm)\).

Vậy \(AH = \frac{{4\sqrt 6 }}{3}\;\,cm;\,\,HB = \frac{{4\sqrt 3 }}{3}\;\,cm\).