Cho tam giác ABC đều, cạnh a, tâm O. Tính |vecto AC - vecto AB - vecto OC|
Cho tam giác ABC đều, cạnh a, tâm O. Tính |→AC−→AB−→OC|.
Cho tam giác ABC đều, cạnh a, tâm O. Tính |→AC−→AB−→OC|.
|→AC−→AB−→OC|
= |→AB+→BC−→AB+→CO|
= |→BC+→CO|
= |→BO|=BO
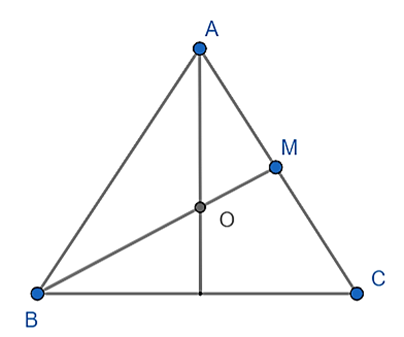
Gọi M là trung điểm AC
Suy ra: BO = 23BM
BM=√AB2−AM2=√a2−(a2)2=a√32
BO = a√32.23=a√33
Vậy |→AC−→AB−→OC|=a√33.