Cho tam giác ABC có hai đường trung tuyến BM, CN vuông với nhau và có BC = 3, góc BAC= 30^0. Tính SΔABC.

Trả lời

Lời giải

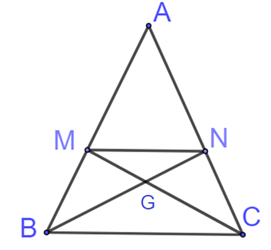
Gọi G là giao điểm của hai đường trung tuyến BM và CN.

Khi đó, G là trọng tâm tam giác ABC.

Áp dụng công thức đường trung tuyến:

• \[B{M^2} = \frac{{{c^2} + {a^2}}}{2} - \frac{{{b^2}}}{4}\]

• \[C{N^2} = \frac{{{a^2} + {b^2}}}{2} - \frac{{{c^2}}}{4}\]

• \[B{G^2} = \frac{4}{9}B{M^2} = \frac{2}{9}({c^2} + {a^2}) - 19{b^2}\]

• \[N{G^2} = \frac{1}{9}C{N^2} = \frac{1}{{18}}({a^2} + {b^2}) - \frac{1}{{36}}{c^2}\]

Theo công thức Py-ta-go, ta có: BN² = BG² + NG²

Áp dụng công thức cos, ta có:

\[\frac{{{c^2}}}{4} = \frac{2}{9}({c^2} + {a^2}) - \frac{1}{9}{b^2} + \frac{1}{{18}}({a^2} + {b^2}) - \frac{1}{{36}}{c^2} = 45\]

\[{a^2} = {b^2} + {c^2} - 2bc\cos A = {b^2} + {c^2} - \sqrt 3 bc\].

Diện tích tam giác ABC là:

\[{S_{ABC}} = \frac{1}{2}bc.sin\widehat A = \frac{1}{2}.12\sqrt 3 .sin30 = 3\sqrt 3 \] (đvdt).