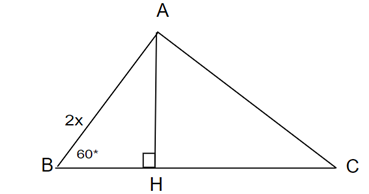
Dựng AH ⊥ BC, đặt AB = x, ta có: AH = x.sinB = x.sin60° = \(x\frac{{\sqrt 3 }}{2}\)

HB = x.cos60° = \(\frac{x}{2}\)⇒ HC = BC – HB = 8 - \(\frac{x}{2} = \frac{{\left( {16 - x} \right)}}{2}\)

AC = 12 – AB = 12 – x

Trong tam giác vuông AHC: \(A{H^2} + H{C^2} = A{C^2}\)

Hay \({\left( {\frac{{x\sqrt 3 }}{2}} \right)^2} + \frac{{{{\left( {16 - x} \right)}^2}}}{4} = {\left( {12 - x} \right)^2}\)

\( \Leftrightarrow 3{x^2} + {\left( {16 - x} \right)^2} = 4{\left( {12 - x} \right)^2}\)

Giải phương trình này tìm được x = 5. Vậy AB = 5 cm.