Cho tam giác ABC có góc B = 120độ, BC = 12 cm, AB = 6 cm. Đường phân giác
Cho tam giác ABC có ˆB=120∘, BC = 12 cm, AB = 6 cm. Đường phân giác của góc B cắt cạnh AC tại D. Gọi M là trung điểm của BC.
Chứng minh AM ⊥ BD.
Cho tam giác ABC có ˆB=120∘, BC = 12 cm, AB = 6 cm. Đường phân giác của góc B cắt cạnh AC tại D. Gọi M là trung điểm của BC.
Chứng minh AM ⊥ BD.
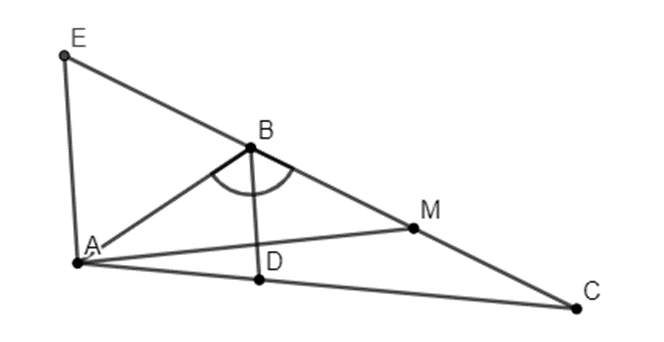
Ta có: ^ABD=^CBD=^ABC2=60∘
Từ A kẻ đường thẳng song song với BD cắt CB tại E.
Lại có:
^BAE=^ABD=60∘ (so le trong)
^CBD=^AEB=60∘ (đồng vị)
Suy ra ΔABEđều ⇒AB = BE = EA = 6 (cm) (1)
MB=MC=12BC=12.12=6(cm) (2)
Từ (1) và (2) suy ra:
BM = AB ⇒ΔABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân).
Vậy BD⊥AM.