Lời giải
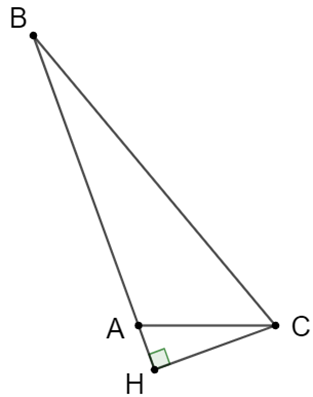
Ta có: \(\widehat {BAC} - \widehat {ABC} = 90^\circ \Rightarrow \widehat {BAC} = 90^\circ + \widehat {ABC}\).
Lại có: \(\widehat {BAC} + \widehat {HAC} = 180^\circ \) (Hai góc kề bù) \( \Rightarrow \widehat {HAC} = 180^\circ - \widehat {BAC}\).
Suy ra \(\widehat {HAC} = 180^\circ - \left( {90^\circ + \widehat {ABC}} \right) = 90^\circ - \widehat {ABC}\) (1)
Xét ∆BHC vuông tại H (Do CH ^ BA) có:
\(\widehat {HBC} + \widehat {BCH} = 90^\circ \Rightarrow \widehat {BCH} = 90^\circ - \widehat {HBC}\) (2)
Từ (1) và (2) suy ra \(\widehat {HAC} = \widehat {BCH}\).
Vậy \(\widehat {HAC} = \widehat {BCH}\) (đpcm).