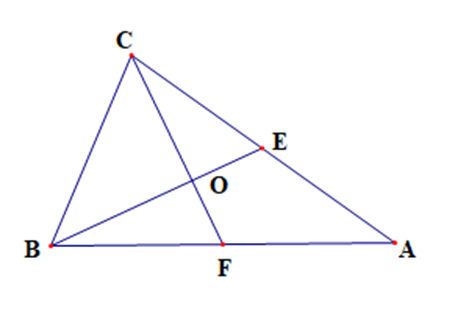
Vì E là trung điểm của AC nên \[AE = EC = \frac{1}{2}AC\]

Vì F là trung điểm của AB nên \[AF = FB = \frac{1}{2}AB\]

Vì O là trọng tâm tam giác ABC, BE và CF là hai tiếp tuyến

Suy ra \[OE = \frac{1}{2}OB,OF = \frac{1}{2}OC\].

Xét tam giác COE vuông ở O có CE² = CO² + OE²

Xét tam giác COB vuông ở O có CB² = CO² + OB²

Xét tam giác FOB vuông ở O có FB² = FO² + OB²

Ta có AB² + AC² = (2BF)² + (2CE)²

= 4BF² + 4CF²

= 4(FO² + OB²) + 4(CO² + OE²)

= 4(CO² + OB²) + 4FO² + 4OE²

\( = 4B{C^2} + 4.\frac{1}{4}.C{O^2} + 4.\frac{1}{4}.O{B^2}\)

= 5BC²

Suy ra AB² + AC² – BC²  = 4BC²

Do đó \(\frac{{A{B^2} + A{C^2} - B{C^2}}}{{2{\rm{AB}}{\rm{.AC}}}} = \frac{{4B{C^2}}}{{2{\rm{A}}B.AC}}\)

Suy ra \(\cos A = \frac{{4B{C^2}}}{{2{\rm{A}}B.AC}} \ge \frac{{4B{C^2}}}{{{\rm{A}}{B^2} + A{C^2}}} = \frac{{4B{C^2}}}{{5B{C^2}}} = \frac{4}{5}\)

Vậy \[cosA \ge \frac{4}{5}\].