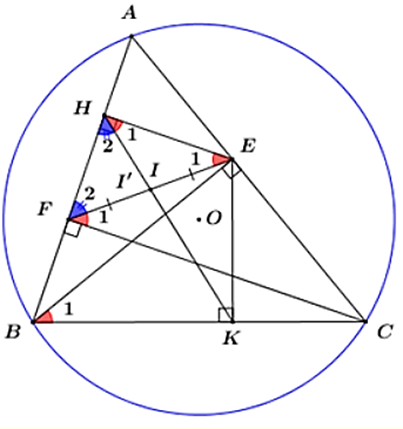
1) Ta có: \(\widehat {BHE} = \widehat {BKE} = 90^\circ \)(vì EH vuông góc AB, EK vuông góc BC)

Xét tứ giác BHEK có: \(\widehat {BHE} + \widehat {BKE} = 90^\circ + 90^\circ = 180^\circ \)

Nên BHEK là tứ giác nội tiếp

2) Ta có: \(\widehat {BHE} + \widehat {EBH} = 90^\circ \)(do tam giác BHE vuông tại H)

\(\widehat {BAE} + \widehat {EBH} = 90^\circ \)(do tam giác ABE vuông tại E)

Nên: \(\widehat {BHE} = \widehat {BAE}\)

Mà \(\widehat {BHE} = \widehat {BKH}\)

Suy ra: \(\widehat {BAE} = \widehat {BKH}\)

Xét tam giác BHK và tam giác BCA có:

\(\widehat B\)chung

\(\widehat {BAE} = \widehat {BKH}\)

⇒ ∆BHK ∽ ∆BCA (g.g)

⇒ \(\frac{{BH}}{{BC}} = \frac{{BK}}{{BA}}\)

⇒ BH.BA = BK.BC

3) Gọi I’ là giao điểm của HK và EF

Xét tứ giác BFEC có: \(\widehat {BFC} = \widehat {BEC} = 90^\circ \)

Nên BFEC là tứ giác nội tiếp

Suy ra: \[\widehat {{B_1}} = \widehat {{F_1}}\](2 góc nội tiếp cùng chắn cung EC)

Ta có: EH // CF (cùng vuông góc AB)

Nên: \[\widehat {{E_1}} = \widehat {{F_1}}\](2 góc so le trong)

Suy ra: \[\widehat {{B_1}} = \widehat {{E_1}}\] (1)

Theo câu a tứ giác BHEK nội tiếp nên \[\widehat {{B_1}} = \widehat {{H_1}}\] (2 góc nội tiếp cùng chắn cung EK) (2)

Từ (1) và (2) suy ra: \[\widehat {{H_1}} = \widehat {{E_1}}\]

Suy ra: I'HE cân tại I' hay I'H = I'E (3)

Lại có: \[\widehat {{H_1}} + \widehat {{H_2}} = 90^\circ \]

\[\widehat {{F_2}} + \widehat {{E_1}} = 90^\circ \] (do tam giác HEF vuông tại H)

Nên: \[\widehat {{H_2}} = \widehat {{F_2}}\]hay tam giác I'HF cân tại I'

Suy ra: I'H = I'F (4)

Từ (3) và (4) suy ra: I'E = I'F hay I' là trung điểm EF

Suy ra: I' ≡ I nên I, H, K thẳng hàng.