Cho tam giác ABC có AM là trung tuyến, I là trung điểm AM a) Chứng minh:
Cho tam giác ABC có AM là trung tuyến, I là trung điểm AM
a) Chứng minh: 2→IA+→IB+→IC=→0
b) Với O bất kỳ, chứng minh: 2→OA+→OB+→OC=4→OI
Cho tam giác ABC có AM là trung tuyến, I là trung điểm AM
a) Chứng minh: 2→IA+→IB+→IC=→0
b) Với O bất kỳ, chứng minh: 2→OA+→OB+→OC=4→OI
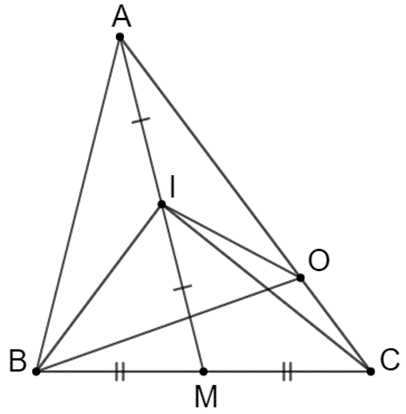
a) Ta có:
2→IA+→IB+→IC=→MA+(→IM+→MB)+(→IM+→MC)
=→MA+(→IM+→IM)+(→MB+→MC)
=→MA+2→IM=→MA+→AM
=→MM=→0
b) 2→IA+→IB+→IC=→0
⇔2(→IO+→OA)+(→IO+→OB)+(→IO+→OC)=→0
⇔(2→OA+→OB+→OC)+(2→IO+→IO+→IO)=→0
⇔(2→OA+→OB+→OC)+4→IO=→0
⇔2→OA+→OB+→OC=4→OI