Cho tam giác ABC có AM là trung tuyến, I là trung điểm AM. a) Chứng minh:
Cho tam giác ABC có AM là trung tuyến, I là trung điểm AM.
a) Chứng minh: 2→IA+→IB+→IC=→0.
b) Với O bất kỳ , chứng minh: 2→OA+→OB+→OC=4→OI.
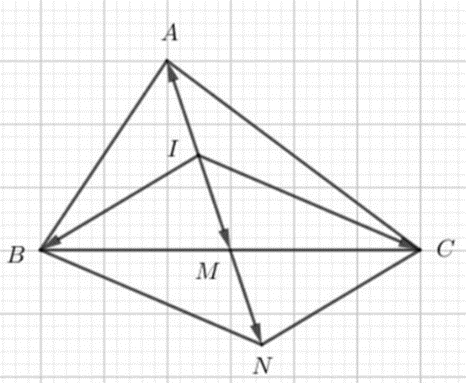
a) Gọi N là điểm đối xứng của I qua M
Suy ra M là trung điểm của IN
Xét tứ giác BICN là BC và IN cắt nhau tại trung điểm M của mỗi đường
Suy ra BICN là hình bình hành
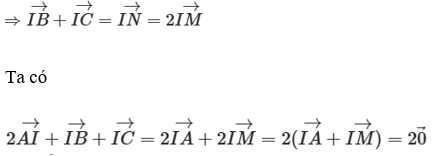
Vậy 2→IA+→IB+→IC=→0
b) Ta có
2→OA+→OB+→OC=2(→OI+→IA)+→OI+→IB+→OI+→IC
=4→OI+2→IA+→IB+→IC=4→OI
Vậy 2→OA+→OB+→OC=4→OI.