Cho tam giác ABC có AB = AC và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho NK = NC.

a) Chứng minh ∆ABM = ∆CMA.

b) Chứng minh AK = 2MC.

c) Tính $\widehat{MAK}$ .

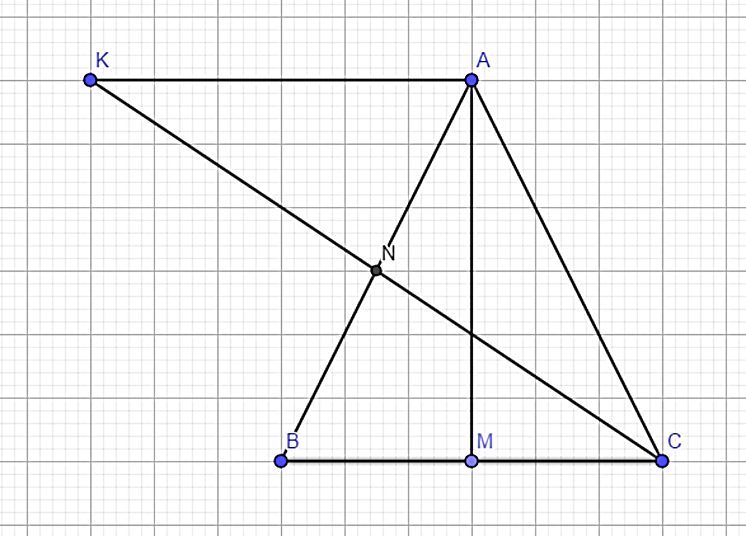
a) Xét hai tam giác ABM và ACM có:

AM chung

AB = AC (theo giả thiết)

BM = MC (do M là trung điểm BC)

Suy ra ΔABM = ΔACM (c.c.c).

b) Xét ΔBNC và ΔANK có:

NB = AN (do N là trung điểm AB)

$\widehat{BNC}=\widehat{ANK}$ (2 góc đối đỉnh)

NC = KN(theo giả thiết)

Suy ra ΔBNC = ΔANK (c.g.c)

Do đó BC = AK (2 cạnh tương ứng)

Mà BC = 2MC ⇒ AK = 2MC.

c) Theo chứng minh phần b thì ΔBNC = ΔANK (c.g.c) nên $\widehat{NBC}=\widehat{NAK}$ (2 góc tương ứng)

Suy ra: AK // BC (do 2 góc trên ở vị trí so le trong)

Mặt khác theo phần a, ΔABM = ΔACM  nên $\widehat{AMB}=\widehat{AMC}$ = 90° ⇒ AM ⊥ BC

Do đó AK ⊥ AM ⇒ $\widehat{MAK}$ = 90°.