Cho tam giác ABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm của
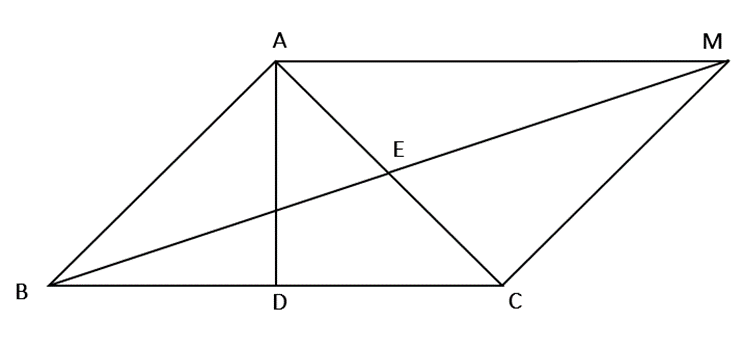
Cho tam giác ABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm của AC, trên tia đối của tia EB lấy điểm M sao cho EM = EB.
a) Chứng minh ∆ABD = ∆ACD;
b) Chứng minh rằng AM = 2.BD;
c) Tính số đo \(\widehat {MAD}\).