Cho tam giác ABC, có AB = AC. AM là tia phân giác của góc A a) Chứng minh
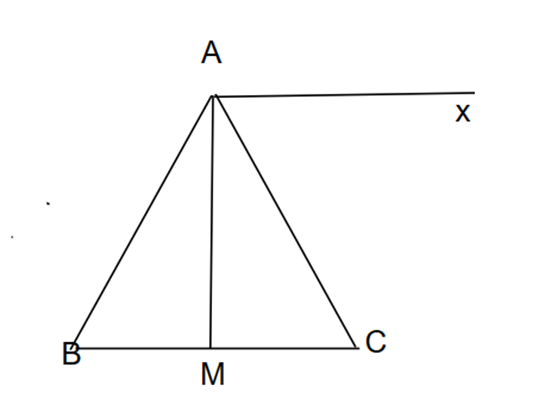
Cho tam giác ABC, có AB = AC. AM là tia phân giác của góc A
a) Chứng minh DAMB = DAMC.
b) Chứng minh M là trung điểm của BC.
c) Cho biết Ax là tia phân giác góc ngoài của đỉnh A. Chứng minh Ax // BC.