Cho tam giác ABC có AB = 2, AC = 3, vecto BAC= 60^0. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn vecto AD = 7/12 vecto AC. a) Tính vecto AB . vecto AC. b) Biểu diễn vecto AM, vec
55
14/05/2024
Cho tam giác ABC có AB = 2, AC = 3, ^BAC=60∘. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn →AD=712→AC.
a) Tính →AB.→AC.
b) Biểu diễn →AM,→BD theo →AB,→AC.
c) Chứng minh AM ⊥ BD.
Trả lời
Lời giải
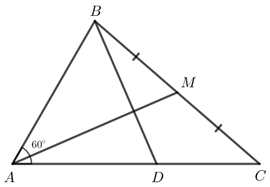
a) Ta có →AB.→AC=|→AB|.|→AC|.cos(→AB,→AC)
=AB.AC.cos^BAC=2.3.cos60∘=3.
Vậy →AB.→AC=3.
b) Vì M là trung điểm BC nên ta có 2→AM=→AB+→AC.
⇔→AM=12→AB+12→AC.
Ta có →BD=→AD−→AB=712→AC−→AB.
Vậy →AM=12→AB+12→AC và →BD=712→AC−→AB.
c) Ta có →AM.→BD=(12→AB+12→AC).(712→AC−→AB)
=724→AB.→AC−12.→AB2+724.→AC2−12→AB.→AC
=−524→AB.→AC−12.AB2+724.AC2
=−524.3−12.22+724.32=0.
Do đó →AM⊥→BD.
Vậy AM ⊥ BD.

