Cho tam giác ABC có AB = 2, AC = 3, vecto BAC = 60 độ. Gọi M là trung điểm của
Cho ∆ABC có AB = 2, AC = 3, ^BAC=60∘. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn →AD=712→AC. Tính →AB.→AC.
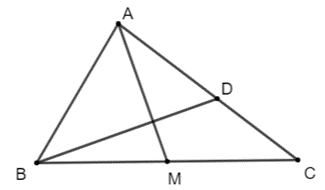
Ta có: →AB.→AC=|→AB|.|→AC|.cos(→AB,→AC)
=AB.AC.cos^BAC=2.3.cos60∘=3