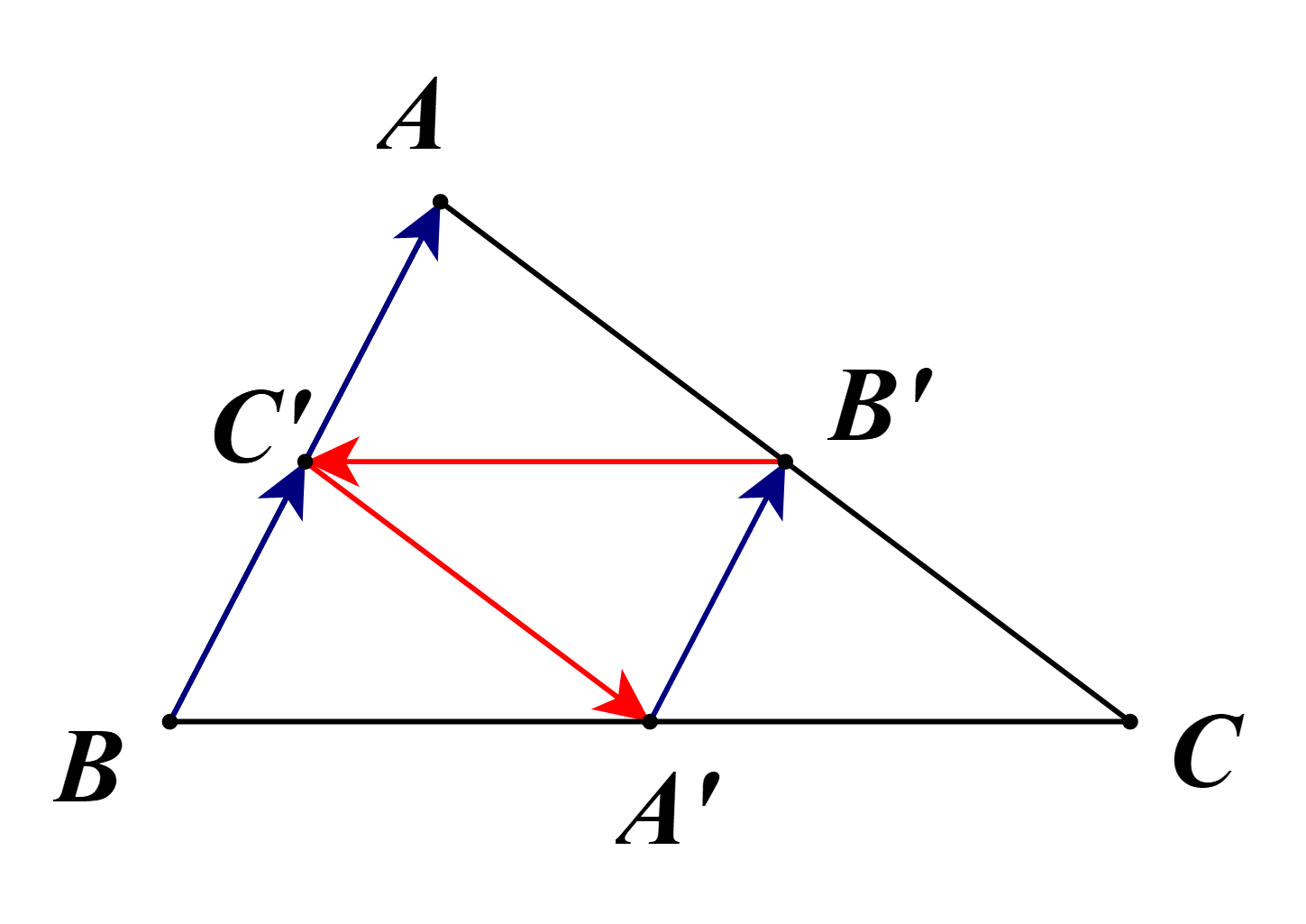
Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của BC, CA, AB. a) Chứng minh vecto BC' = vecto C'A = vecto A'B'. b) Tìm các vectơ bằng vecto B'C', vecto C'A'
28
14/05/2024
Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của BC, CA, AB.
a) Chứng minh \(\overrightarrow {BC'} = \overrightarrow {C'A} = \overrightarrow {A'B'} \).
b) Tìm các vectơ bằng \(\overrightarrow {B'C'} ,\,\overrightarrow {C'A'} \).
Trả lời
Lời giải
a) Tam giác ABC có A’B’ là đường trung bình.
Suy ra A’B’ = BC’ = C’A.
Mà \(\overrightarrow {BC'} ,\,\overrightarrow {C'A} ,\,\overrightarrow {A'B'} \) cùng phương với nhau.
Vậy \(\overrightarrow {BC'} = \overrightarrow {C'A} = \overrightarrow {A'B'} \).
b) Tương tự câu a, ta có \(\overrightarrow {A'B} = \overrightarrow {CA'} = \overrightarrow {B'C'} \) và \(\overrightarrow {AB'} = \overrightarrow {B'C} = \overrightarrow {C'A'} \).
