Cho tam giác ABC. Chứng minh điều kiện cần và đủ để hai trung tuyến BM và CN vuông góc với nhau là b^2 +  c^2 = 5a^2.

Trả lời

Lời giải

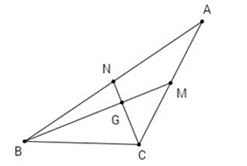
Gọi G  là giao điểm của hai trung tuyến BM, CN.

Áp dụng công thức tính trung tuyến, ta có:

• $G{B^2} = \frac{4}{9}B{M^2} = \frac{1}{9}\left( {2{a^2} + 2{c^2} - {b^2}} \right)$;

• $G{C^2} = \frac{4}{9}C{N^2} = \frac{1}{9}\left( {2{a^2} + 2{b^2} - {c^2}} \right)$.

BM và CN vuông góc với nhau khi BG² + CG² = BC².

$\Leftrightarrow \frac{1}{9}\left( {2{a^2} + 2{c^2} - {b^2}} \right) + \frac{1}{9}\left( {2{a^2} + 2{b^2} - {c^2}} \right) = {a^2}$

Û 4a² + b² + c² = 9a²

Û b² +  c² = 5a².