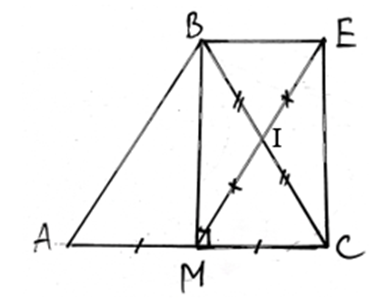
a. Xét tứ giác BMCE có 2 đường chéo

BC và ME cắt nhau tại trung điểm I của mỗi đường

⇒ Tứ giác BMCE là hình bình hành (1)

Vì ∆BAC cân tại B có M là trung điểm của AC ⇒ trung tuyến BM đồng thời là đồng thời là đường cao ⇒ $\widehat {BMC} = 90^\circ$ (2)

Từ (1) và (2) ⇒ Tứ giác BMCE là hình chữ nhật.

b. Vì tứ giác BMCE là hình chữ nhật (cmt) ⇒ BE // MC

BE = MC; MC = MA ⇒ MA = BE

Có BE // MC ⇒ BE // AM (vì M ∈ AC)

Xét tứ giác ABEM có: $\left\{ {\begin{array}{*{20}{c}}{BE//AM}\\{BE = AM}\end{array}} \right.$ ⇒ tứ giác ABEM là hình bình hành.

Vậy tứ giác ABEM là hình bình hành.

c. Tứ giác MCEB là hình vuông

Khi MB = MC ⇒ ∆BMC là tam giác vuông cân

$\Rightarrow \widehat {MBC} = 45^\circ = \frac{{\widehat {ABC}}}{2} \Rightarrow \widehat {ABC} = 2\widehat {MBC} = 2.45^\circ = 90^\circ$

⇒ ∆BAC là tam giác vuông cân

⇒ Tứ giác MCBE là hình vuông khi ∆BAC là tam giác vuông cân tại B.