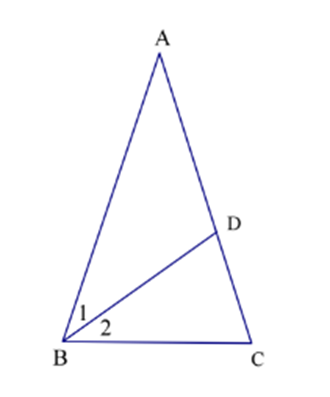
Kẻ phân giác BD của $\widehat {ABC}$(D thuộc AC).

Khi đó: $\widehat {{B_1}} = \widehat {B2} = 36^\circ$

Suy ra: tam giác ABD cân tại D và tam giác BCD cân tại B

Nên AD = BC = BD

Theo tính chất đường phân giác trong tam giác ABC có:

$\frac{{BA}}{{BC}} = \frac{{AC}}{{CD}}$ ⇒ $\frac{{BA}}{{BC}} = \frac{{BC}}{{AC - AD}}$

Mà AB = AC; AD = BC

Nên $\frac{{BA}}{{BC}} = \frac{{BC}}{{BA - BC}}$ ⇔ BA(BC – BC) = BC²

⇔ AB² – BA.BC = BC²

⇔ AB² = AB.BC + BC²