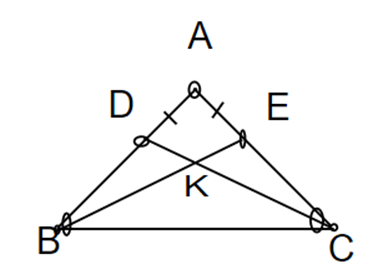
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao
Cho ∆ABC cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE.
a. Chứng minh rằng BE = CD.
b. Chứng minh rằng ^ABE=^ACD.
c. Gọi K là giao điểm của BE và CD. ∆KBC là tam giác gì? Vì sao?