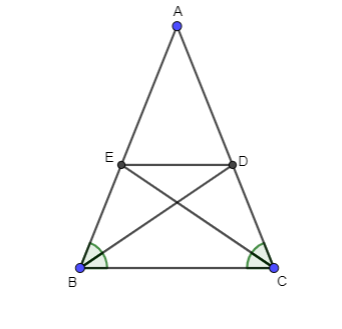
Cho tam giác ABC cân tại A . Tia giác góc B cắt cạnh AC tại D, tia phân giác góc C cắt cạnh AB tại E.
Cho cân tại A . Tia giác góc B cắt cạnh AC tại D, tia phân giác góc C cắt cạnh AB tại E. Chứng minh cân.

cân tại A nên (t/c tam giác cân)
Mà
Nên
Xét và có:
(cmt)
BC là cạnh chung
(cmt)
Do đó, (g.c.g)
BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
AE = AD
cân tại A (đpcm)