Cho tam giác ABC cân tại A, góc A bé hơn 90°. Kẻ AB vuông góc AC. Trên AB lấy E sao cho AE bằng AD. Chứng minh rằng:

a) DE song song BC.

b) CE vuông góc AB.

Lời giải

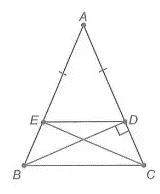
a) Vì tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\)

Xét tam giác ABC có \(\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = 180^\circ \)(tổng ba góc trong một tam giác)

Mà \(\widehat {ABC} = \widehat {ACB}\) (chứng minh trên)

Suy ra \(\widehat {ABC} = \frac{{180^\circ - \widehat {BAC}}}{2}\)                            (1)

Vì AE = AD nên tam giác AED cân tại A

Suy ra \(\widehat {ADE} = \widehat {AE{\rm{D}}}\)

Xét tam giác ADE có \(\widehat {ADE} + \widehat {AE{\rm{D}}} + \widehat {DA{\rm{E}}} = 180^\circ \)(tổng ba góc trong một tam giác)

Mà \(\widehat {ADE} = \widehat {AE{\rm{D}}}\) (chứng minh trên)

Suy ra \(\widehat {AE{\rm{D}}} = \frac{{180^\circ - \widehat {BAC}}}{2}\)                       (2)

Từ (1) và (2) suy ra \(\widehat {ABC} = \widehat {AE{\rm{D}}}\)

Mà hai góc này ở vị trí đồng vị

Suy ra ED // BC

Vậy ED // BC.

b) Xét tam giác ABD và tam giác ACE có

AB = AC (chứng minh câu a)

\(\widehat A\)là góc chung

AE = AD (giả thiết)

Do đó △ ABD = △ ACE (c.g.c)

Suy ra \(\widehat {AEC} = \widehat {ADB}\) (hai góc tương ứng)

Mà \(\widehat {ADB} = 90^\circ \) (vì AD ⊥ BC)

Nên \(\widehat {AEC} = 90^\circ \)

Hay CE ⊥ BA

Vậy CE ⊥ BA.