Cho tam giác ABC cân tại A có đường cao AD, O là trung điểm AC, điểm E đối xứng với điểm D qua điểm O. a) Chứng minh tứ giác AECD là hình chữ nhật. b) Gọi I là trung điểm AD, Chứng minh I l
30
12/05/2024
Cho tam giác ABC cân tại A có đường cao AD, O là trung điểm AC, điểm E đối xứng với điểm D qua điểm O.
a) Chứng minh tứ giác AECD là hình chữ nhật.
b) Gọi I là trung điểm AD, Chứng minh I là trung điểm BE.
Trả lời
Lời giải:
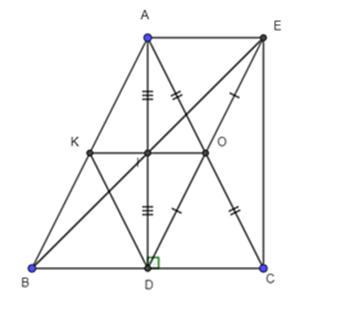
a) Vì O là trung điểm AC nên O là trung điểm của DE (E đối D qua O).
Suy ra AECD là hình bình hành (định nghĩa hình bình hành).
Mà \[\widehat {ADC}\] = 90° (AD ⊥ BC).
Do đó AECD là hình chữ nhật.
b) Vì AECD là hình chữ nhật (chứng minh trên).
Nên AE = CD và AE // CD (tính chất hình bình hành).
Mà DC = BD (D trung điểm BC do AD ⊥ BC, ΔABC cân tại A).
Do đó: AE // BD (B ∈ CD), AE = BD.
Suy ra AEDB là hình bình hành (định nghĩa hình bình hành)
Mà I là trung điểm AD nên I là trung điểm BE (tính chất hình bình hành).

