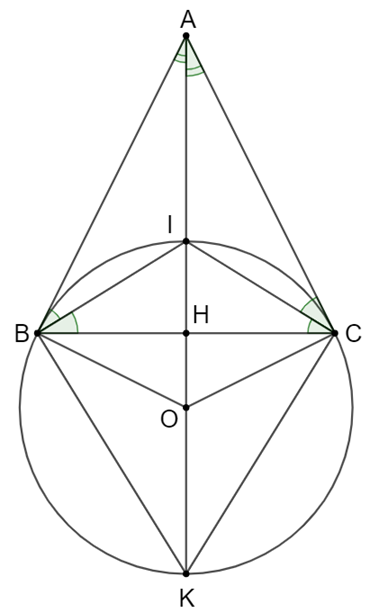
Cho tam giác ABC cân ở A. Gọi I là giao điểm các đường phân giác. a) Xác định vị trí tương đối của đường thẳng AC với đường tròn (O) ngoại tiếp ∆BIC
Cho tam giác ABC cân ở A. Gọi I là giao điểm các đường phân giác.
a) Xác định vị trí tương đối của đường thẳng AC với đường tròn (O) ngoại tiếp ∆BIC