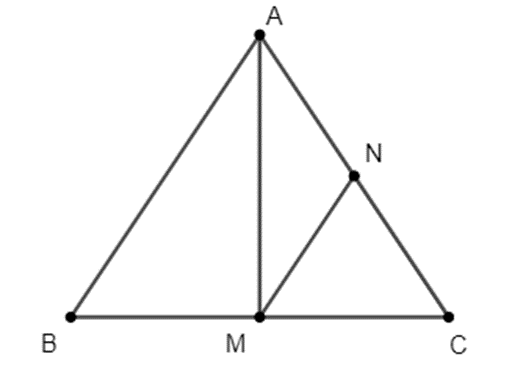
Cho tam giác ABC câCho tam giác ABC cân tại A (AB = AC). M là trung điểm của BC. a) Chứng minhn tại A (AB = AC). M là trung điểm của BC. a) Chứng minh
Cho tam giác ABC cân tại A (AB = AC). M là trung điểm của BC.
a) Chứng minh ∆AMB = ∆AMC và ^BAM=^CAM
b) Qua M kẻ đường thẳng song song với AB cắt AC tại N. Chứng minh ∆MNC cân.
c) Chứng minh: N trung điểm của AC.