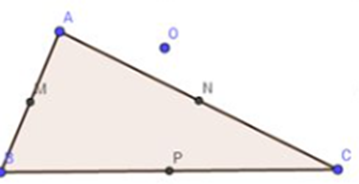
Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chứng minh rằng với điểm O bất kì, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \).
Vì M là trung điểm của AB nên \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} \)
Vì N là trung điểm của AC nên \(\overrightarrow {OA} + \overrightarrow {OC} = 2\overrightarrow {ON} \)
Vì P là trung điểm của BC nên \(\overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {OP} \)
Suy ra \(2\overrightarrow {OA} + 2\overrightarrow {OB} + 2\overrightarrow {OC} = 2\overrightarrow {OM} + 2\overrightarrow {ON} + 2\overrightarrow {OP} \)
Hay \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \)
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \).