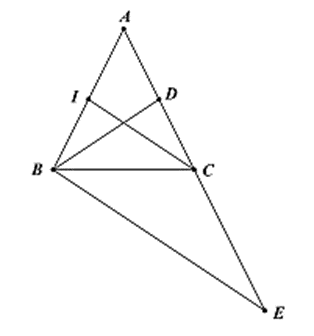
Cho tam giác ABC (AB = AC), trung tuyến BD. Lấy điểm E sao cho C là trung điểm AE. Gọi I là trung điểm AB. Chứng minh rằng:
a) AD = AI.
b) BE = 2CI.
c) ∆ABD = ∆ACI.
d) BE = 2BD.
a) Tam giác ABC có BD là đường trung tuyến.
Suy ra D là trung điểm AC. Do đó AC = 2AD (1)
Lại có I là trung điểm AB (giả thiết). Suy ra AB = 2AI (2)
Ta có AB = AC (giả thiết) (3)
Từ (1), (2), (3), suy ra 2AD = 2AI.
Vậy AD = AI.
b) Tam giác ABE có C, I lần lượt là trung điểm của AE, AB.
Suy ra CI là đường trung bình của tam giác ABE.
Vậy BE = 2CI.
c) Xét ∆ABD và ∆ACI có:
AB = AC (giả thiết)
\(\widehat {BAC}\)là góc chung
AD = AI (kết quả câu a)
Suy ra: ∆ABD = ∆ACI (c.g.c)
d) Ta có: BD = CI do ∆ABD = ∆ACI
Mà BE = 2CI (theo b)
Nên BE = 2BD.