Cho tam giác ABC (AB > AC) có đường cao AH . Gọi M , N, P lần lượt là trung
Cho tam giác ABC (AB > AC) có đường cao AH . Gọi M , N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh: NP là đường trung trực của AH.
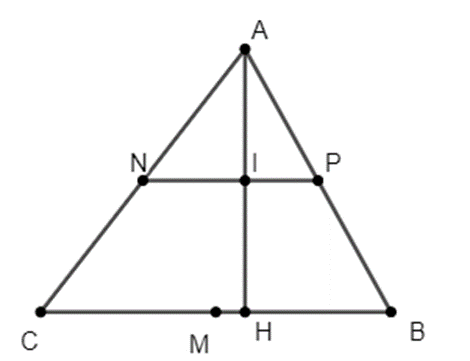
Gọi I là giao điểm của AH và PN.
Xét ∆ABC có: AP = BP và AN = NC.
Do đó PN là đường trung bình của \(\Delta \)ABC
Suy ra PN // BC mà AH\( \bot \)BC
Do đó PN\( \bot \)AH (1)
Ta có: PN // BC mà PI ∈ PN
Suy ra PI // BC
Xét ∆AHB có: PI // BC và AP = BP
Suy ra AI = IH (2)
Từ (1) và (2) suy ra PN là đường trung trực của AH.