Cho phương trình x² – 2x – 2m² = 0 (m là tham số).

a) Giải phương trình khi m = 0.

 b) Tìm m để phương trình có hai nghiệm x₁, x₂ khác 0 và thỏa mãn điều kiện $x_1^2 = 4x_2^2$.

Lời giải

a) Khi m = 0 ta có phương trình x² – 2x = 0

Û x(x – 2) = 0

Û $\left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.$

Vậy khi m = 0, phương trình có tập nghiệm S = {0; 2}.

b) Phương trình x² – 2x – 2m² = 0 (1)

Phương trình (1) có hai nghiệm phân biệt x₁, x₂ khác 0 Û $\left\{ \begin{array}{l}\Delta ' > 0\\{x_1}.{x_2} \ne 0\end{array} \right.$

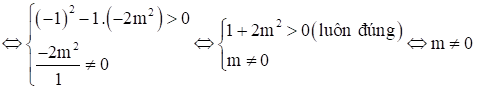
Theo hệ thức Viet ta có:

$\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}.{x_2} = - 2{m^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 2 - {x_1}\,\,\,\,\,\\{x_1}.{x_2} = - 2{m^2}\,\,\left( * \right)\end{array} \right.$

Do x₁, x₂ là hai nghiệm của phương trình (1) nên ta có:

$\left\{ \begin{array}{l}{\rm{x}}_1^2--2{x_1}--2{m^2} = 0\\{\rm{x}}_2^2--2{x_2}--2{m^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\rm{x}}_1^2 = 2{x_1} + 2{m^2}\\{\rm{x}}_2^2 = 2{x_2} + 2{m^2}\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}{\rm{x}}_1^2 = 2{x_1} + 2{m^2}\\{\rm{x}}_2^2 = 2\left( {2 - {x_1}} \right) + 2{m^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\rm{x}}_1^2 = 2{x_1} + 2{m^2}\\{\rm{x}}_2^2 = 4 - 2{x_1} + 2{m^2}\end{array} \right.$

Theo bài, $x_1^2 = 4x_2^2$

Û 2x₁ + 2m² = 4.(4 – 2x₁ + 2m²)

Û 2x₁ + 2m² = 16 – 8x₁ + 8m²

Û 10x₁ = 6m² + 16

Û ${x_1} = \frac{{3{m^2} + 8}}{5}$

Khi đó ${x_2} = 2 - \frac{{3{m^2} + 8}}{5} = \frac{{2 - 3{m^2}}}{5}$

Thay ${x_1} = \frac{{3{m^2} + 8}}{5}$ và ${x_2} = \frac{{2 - 3{m^2}}}{5}$vào (*) ta được:

$\frac{{3{m^2} + 8}}{5}.\frac{{2 - 3{m^2}}}{5} = - 2{m^2}$

Û 6m² – 9m⁴ + 16 – 24m² = ‒50m²

Û 32m² – 9m⁴ + 16 = 0

$\Leftrightarrow \left[ \begin{array}{l}{m^2} = 4\\{m^2} = - \frac{4}{9}\,\,\,\left( {loai} \right)\end{array} \right. \Leftrightarrow m = \pm 2\left( {tm\,\,m \ne 0} \right)$.

Vậy m = ± 2.