Cho $P = \frac{{2x + 2}}{{\sqrt x }} + \frac{{x\sqrt x - 1}}{{x - \sqrt x }} - \frac{{x\sqrt x + 1}}{{x + \sqrt x }}\,\,\,\left( {x > 0,\,x \ne 1} \right)$.

a) Rút gọn P.

b) So sánh P với 5.

c) Tìm x sao cho $\frac{8}{P}$ nhận giá trị nguyên.

Lời giải

a) $P = \frac{{2x + 2}}{{\sqrt x }} + \frac{{x\sqrt x - 1}}{{x - \sqrt x }} - \frac{{x\sqrt x + 1}}{{x + \sqrt x }}$

$= \frac{{2x + 2}}{{\sqrt x }} + \frac{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}} - \frac{{\left( {\sqrt x + 1} \right)\left( {x - \sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x + 1} \right)}}$

$= \frac{{2x + 2}}{{\sqrt x }} + \frac{{x + \sqrt x + 1}}{{\sqrt x }} - \frac{{x - \sqrt x + 1}}{{\sqrt x }}$

$= \frac{{2x + 2 + x + \sqrt x + 1 - \left( {x - \sqrt x + 1} \right)}}{{\sqrt x }}$

$= \frac{{2x + 2 + 2\sqrt x }}{{\sqrt x }}$.

b) Ta có $P - 5 = \frac{{2x + 2 + 2\sqrt x }}{{\sqrt x }} - 5 = \frac{{2x + 2 - 4\sqrt x + \sqrt x }}{{\sqrt x }}$

$= \frac{{2{{\left( {\sqrt x - 1} \right)}^2} + \sqrt x }}{{\sqrt x }} = \frac{{2{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }} + 1 \ge 1 > 0,\,\forall x$.

Vậy P > 5.

c) $\frac{8}{P} = \frac{{8\sqrt x }}{{2x + 2 + 2\sqrt x }} = \frac{{4\sqrt x }}{{x + 1 + \sqrt x }} = \frac{4}{{\sqrt x + \frac{1}{{\sqrt x }} + 1}}$.

Ta có $\frac{8}{P}$ nhận giá trị nguyên ⇔ $4 \vdots \left( {\sqrt x + \frac{1}{{\sqrt x }} + 1} \right)$.

Ta có Ư(4) ∈ {±1; ±2; ±4}.

Ta có bảng sau:

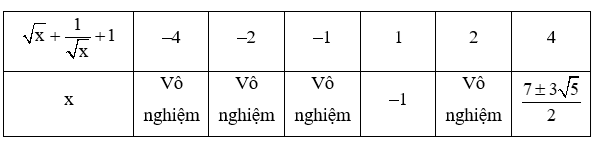
So với điều kiện ban đầu, ta nhận $x \in \left\{ {\frac{{7 \pm 3\sqrt 5 }}{2}} \right\}$.