Cho P = ((2x + 1) / (x căn bậc hai x - 1) - căn bậc hai x / (x + x căn bạc hai x + 1)
Cho P=(2x+1x√x−1−√xx+√x+1)(1+√x31+√x−√x)
a) Rút gọn biểu thức P.
b) Tìm x để P = 3.
Cho P=(2x+1x√x−1−√xx+√x+1)(1+√x31+√x−√x)
a) Rút gọn biểu thức P.
b) Tìm x để P = 3.
a) Điều kiện xác định x≥0,x≠1
Ta có :
P=(2x+1x√x−1−√xx+√x+1)(1+√x31+√x−√x)
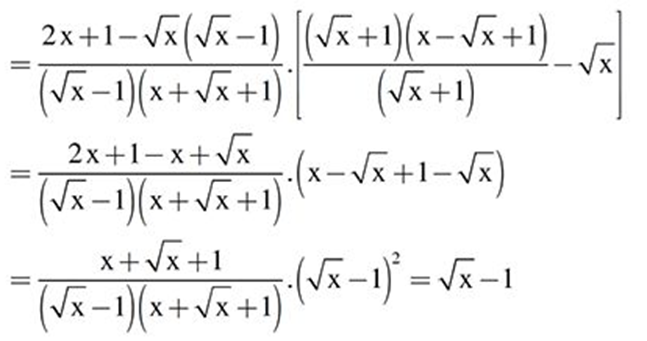
Vậy với x≥0,x≠1 thì P=√x−1.
b) Với x≥0,x≠1 để P = 3 thì √x−1=3
⇔√x=4⇔x=16 (thỏa mãn)
Vậy x = 16 thì P = 3.