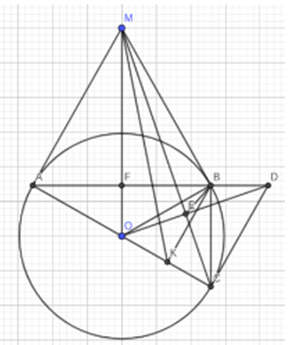
Cho (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB tới đường tròn (O) với A, B là các tiếp điểm. Chứng minh 4 điểm A, B, M, O cùng thuộc 1 đường tròn.
Cho (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB tới đường tròn (O) với A, B là các tiếp điểm. Chứng minh 4 điểm A, B, M, O cùng thuộc 1 đường tròn.