Cho (O) và điểm I bên ngoài (O). Từ I vẽ một cát tuyến IAB với (O). Tiếp tuyến tại A và B cắt nhau tại M. AB cắt OM tại H.
a) Chứng minh: MA2 = MH.MO.
b) Từ M kẻ ME vuông góc OI tại E cắt (O) tại D và AB tại K. Chứng minh: IE.IO = IH.IK.
c) Chứng minh: ID là tiếp tuyến (O).
Lời giải
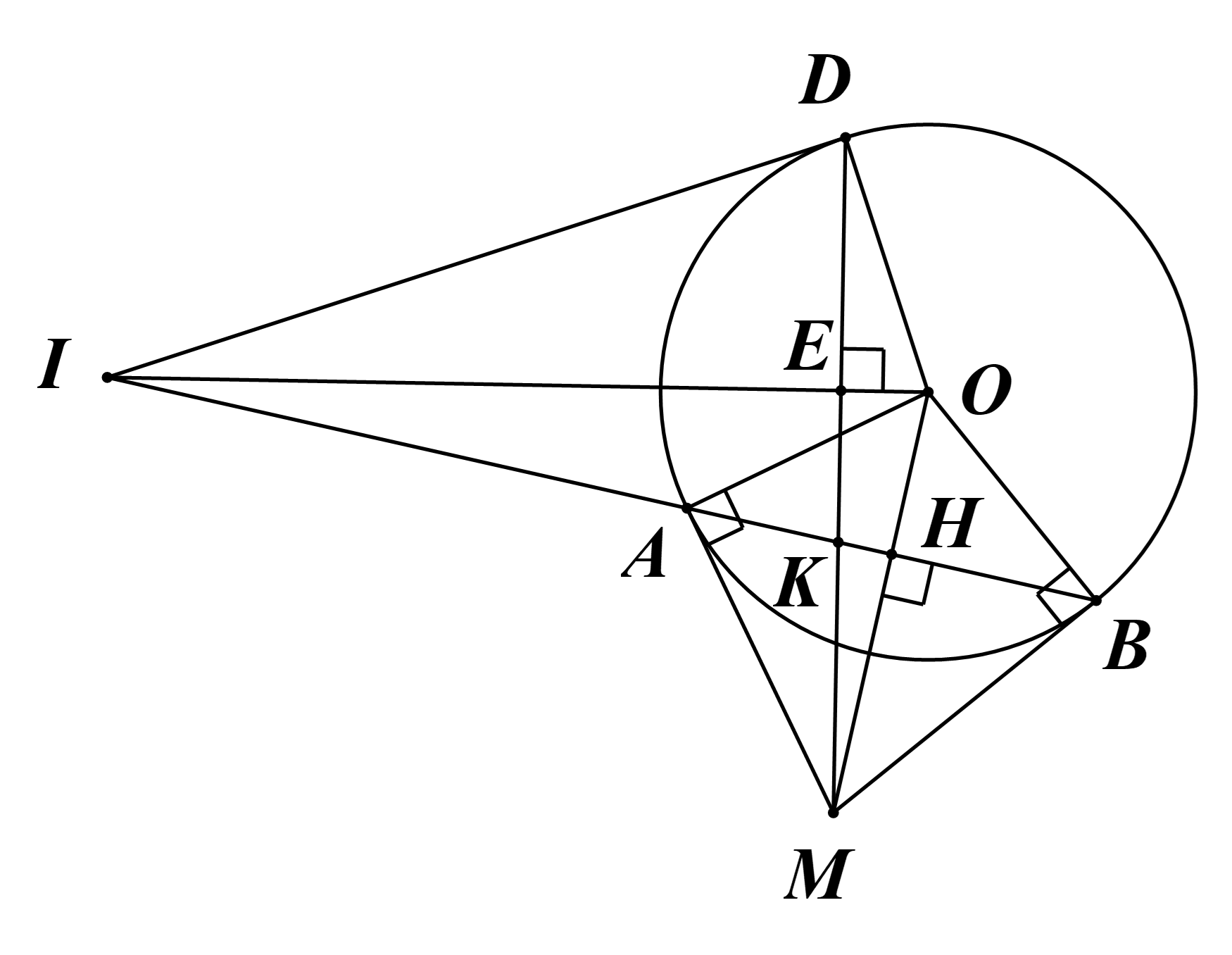
a) Ta có MA, MB là hai tiếp tuyến của (O) cắt nhau tại M.
Suy ra MA = MB.
Khi đó M nằm trên đường trung trực của đoạn thẳng AB (1)
Lại có OA = OB = R.
Suy ra O nằm trên đường trung trực của đoạn thẳng AB (2)
Từ (1), (2), suy ra MO là đường trung trực của đoạn thẳng AB.
Do đó MO ⊥ AB tại H và H là trung điểm AB.
Ta có MA là tiếp tuyến của (O).
Suy ra \(\widehat {AOM} = 90^\circ \).
Xét ∆AOM vuông tại A có AH là đường cao:
MA2 = MH.MO (hệ thức lượng trong tam giác vuông).
b) Xét ∆IEK và ∆IHO, có:
\(\widehat {IEK} = \widehat {IHO} = 90^\circ \).
\(\widehat I\) chung.
Do đó (g.g).
Suy ra \(\frac{{IE}}{{IH}} = \frac{{IK}}{{IO}}\).
Do đó IE.IO = IH.IK.
c) Xét ∆OEM và ∆OHI, có:
\(\widehat {OEM} = \widehat {OHI} = 90^\circ \).
\(\widehat O\) chung.
Do đó (g.g).
Suy ra \(\frac{{OE}}{{OH}} = \frac{{OM}}{{OI}}\).
Do đó OE.OI = OM.OH.
Xét ∆AOM vuông tại A có AH là đường cao:
OA2 = OH.OM (hệ thức lượng trong tam giác vuông).
Suy ra OE.OI = OA2.
Mà OA = OD = R.
Do đó OE.OI = OD2.
Xét ∆ODI và ∆OED, có:
\(\frac{{OD}}{{OE}} = \frac{{OI}}{{OD}}\) (OE.OI = OD2).
\(\widehat O\) chung.
Do đó (c.g.c).
Suy ra \(\widehat {ODI} = \widehat {OED} = 90^\circ \).
Do đó OD ⊥ DI.
Vậy ID là tiếp tuyến của (O).