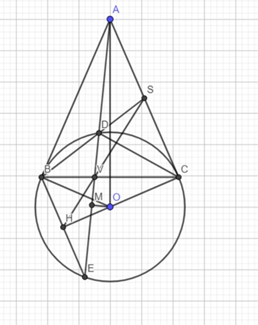
Cho (O; R) và điểm A nằm ngoài đường tròn với OA > 2R. Từ A vẽ 2 tiếp tuyến
Cho (O; R) và điểm A nằm ngoài đường tròn với OA > 2R. Từ A vẽ 2 tiếp tuyến AB, AC của đường tròn (O) (B, C là tiếp điểm). Vẽ dây BE của đường tròn (O) song song với AC; AE cắt (O) tại D khác E; BD cắt AC tại S. Gọi M là trung điểm của đoạn DE.
a. Chứng minh 5 điểm A, B, C, O, M cùng thuộc 1 đường tròn
b. Chứng minh SC2= SB.SD
c. 2 đường thẳng DE và BC cắt nhau tại V; đường thẳng SV cắt BE tại H. Chứng minh 3 điểm H, O, C thẳng hàng.