Cho (O; R) và 3 dây AB, AC, AD; gọi M và N lần lượt là hình chiếu của B trên các đường thẳng AC, AD. Chứng minh MN ≤ 2R.

Trả lời

Lời giải

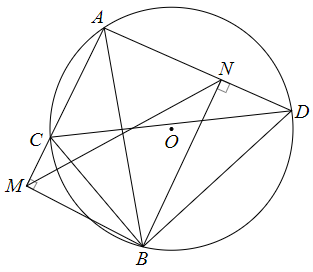
Xét ∆BMC và ∆BND, có:

$\widehat {BMC} = \widehat {BND} = 90^\circ$;

$\widehat {BCM} = \widehat {BDN}$ (bốn điểm A, B, C, D cùng thuộc đường tròn (O; R)).

Do đó  (g.g).

Suy ra $\frac{{BM}}{{BN}} = \frac{{BC}}{{BD}}$ và $\widehat {MBC} = \widehat {NBD}$.

Xét ∆BNM và ∆BDC, có:

$\frac{{BM}}{{BC}} = \frac{{BN}}{{BD}}$ $\left( {\frac{{BM}}{{BN}} = \frac{{BC}}{{BD}}} \right)$.

$\widehat {MBN} = \widehat {CDB}$ (do $\widehat {MBC} + \widehat {CBN} = \widehat {CBN} + \widehat {NBD}$).

Do đó  (c.g.c).

Suy ra $\frac{{MN}}{{CD}} = \frac{{BN}}{{BD}} \le \frac{{BD}}{{BD}} = 1$.

Khi đó MN ≤ CD.

Mà CD ≤ 2R (CD là một dây của đường tròn (O; R)).

Vậy MN ≤ 2R (điều phải chứng minh).