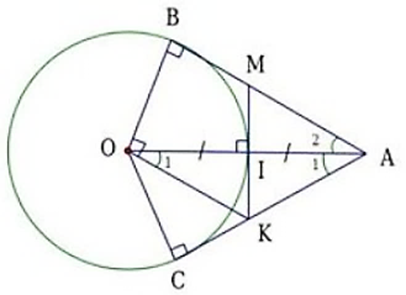
Cho (O; R), lấy điểm A cách O một khoảng bằng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I.
Cho (O; R), lấy điểm A cách O một khoảng bằng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a) Chứng minh: ∆OBA vuông tại B và ∆OAK cân tại K.
a) Chứng minh: ∆OBA vuông tại B và ∆OAK cân tại K.